Contenido

Trabajo Práctico 2

Universidad Tecnológica Nacional - Facultad Regional San Nicolás

Materia: Análisis Matemático 2

Fecha: 31-10-2021

Alumnos

  • Goran Prpic. Ingeniería Electrónica.

  • Pablo Usero. Ingeniería Mecánica.

  • Santiago Asenjo. Ingeniería Electrónica.

Video

La explicación de este TP en video, pedido como parte de la consigna está subido en Youtube al siguiente link:

https://youtu.be/CYrv6CWdzLc

Consigna

Preparar un VIDEO en el que se muestre el proceso de modelización y resolución, por parte de los integrantes del equipo, de DOS PROBLEMAS que se modelicen con DISTINTOS TIPOS DE ECUACIONES DIFERENCIALES ORDINARIAS DE PRIMER ORDEN.

En el video se debe mostrar:

  1. Enunciado de la situación planteada.

  2. Modelo matemático obtenido (ecuación diferencial ordinaria de primer orden) a partir del enunciado.

  3. Resolución y obtención de la solución general.

  4. Proposición de una condición inicial y obtención de la solución particular correspondiente.

  5. Análisis las soluciones obtenidas en función del problema.

  6. interpretación geométrica de las soluciones obtenidas.

Forma de trabajo

Se realiza en EQUIPO conformado por 2 o 3 estudiantes (pueden pertenecer a especialidades distintas)

Atención

Fecha límite de entrega: 01-11-21 (23:59 h)

Atención

El enunciado del problema no debe presentar la ecuación diferencial que modeliza la situación, sino que a partir de los datos del problema se obtenga la modelización del este.

Atención

  • Se podrá buscar el problema tanto en libros de AMII como en Internet. Indicar fuente bibliográfica.

  • Entregar un archivo PDF en donde se incluya: nombre de los participantes del equipo, especialidad y link del video subido en la nube (YouTube o OneDrive).

  • Sólo uno de los integrantes del equipo sube la tarea.

Ejercicio 1

Bronson, R. y Costa, G. (año). Capítulo 7: Aplicaciones de las ecuaciones diferenciales de primer orden. Ecuaciones Diferenciales. Mc Graw Hill.

Enunciado

Cinco ratones de una población estable de 500 son infectados intencionalmente con una enfermedad contagiosa para probar una teoría de difusión de epidemia que postula que la tasa de cambio en la población infectada es proporcional al producto del número de ratones que tienen la enfermedad con el número que está libre de ésta. Asumiendo que la teoría es correcta, ¿cuánto tiempo le tomará a la mitad de la población adquirir la enfermedad?

Ratones

Imagen ilustrativa. Criver

Desarrollo

Sea \(R(t)\) el número de ratones infectados con la enfermedad en el tiempo \(t\). Luego, se dice que en un inicio se infectan 5 ratones, por lo que se deduce que \(R(0) = 5\). Por último, sea \(500 - R(t)\) el número de ratones libre de la enfermedad.

La teoría de difusión de epidemia plantea lo siguiente:

La tasa de cambio en la población infectada es proporcional al producto del número de ratones que tienen la enfermedad con el número que está libre de ésta

Modelo matemático

Lo cual se modeliza con el siguiente modelo matemático:

(1)\[\frac {dR}{dt} = k R (500 - R)\]

O también:

(2)\[\frac {1}{R (500 - R)} dR = k dt\]

Vemos que la forma tomada es la de una ecuación diferencial ordinaria de primer orden a variable separables.

Para resolverla, primero descomponemos en fracciones simples la fracción del primer miembro:

\[\begin{split}\frac {A}{R} + \frac {B}{500 - R} &= \frac {A(500 - R) + B R}{R (500 - R)} \\ &= \frac {1}{R (500 - R)}\end{split}\]

Por lo tanto:

\[ \begin{align}\begin{aligned}1 = A(500 - R) + B R\\R=0 => A = \frac {1}{500}\\R=500 => B = \frac {1}{500}\end{aligned}\end{align} \]

Finalmente:

(3)\[\frac {1}{R (500 - R)} = \frac {1}{500} ( \frac {1}{R} + \frac {1}{500 - R} )\]

Reemplazo (3) en (2).

\[ \begin{align}\begin{aligned}\frac {1}{500} ( \frac {1}{R} + \frac {1}{500 - R} ) dR = k dt\\( \frac {1}{R} + \frac {1}{500 - R} ) dR = 500 k dt\end{aligned}\end{align} \]

Integro ambos miembros

\[\int ( \frac {1}{R} + \frac {1}{500 - R} ) dR = 500 k \int dt\]
\[\ln |R| - \ln |500 - R| = 500kt + C_1\]
\[\ln | \frac {R}{500-R} | = 500kt + C_1\]
\[\frac {R}{500-R} = e^{500kt + C_1}\]
\[\frac {R}{500-R} = e^{500kt} e^{C_1}\]
(4)\[\frac {R}{500-R} = C e^{500kt}\]

Reacomodando:

\[\frac {1}{\frac {500}{R} -1} = C e^{500kt}\]
\[\frac {500}{R} = \frac {1}{C e^{500kt}} + 1\]

Solución general

Despejando \(R(t)\) nos queda la solución general a nuestro modelo matemático planteado:

(5)\[R_{(t)} = \frac {500}{ \frac {1}{C e^{500kt}} + 1 }\]

Para calcular \(C\), traeremos nuevamente la condicion inicial dada por el enunciado \(R(t=0) = 5\) y la reemplazamos en (4) por practicidad:

\[\frac {5}{500-5} = C e^{500 k · 0}\]
\[\frac {5}{495} = C\]
\[C = \frac {1}{99}\]

Por lo que sustituyendo \(C\) en (5) y reacomodando nos queda:

(6)\[R_{(t)} = \frac {500}{ \frac {99}{e^{500kt}} + 1 }\]

Para determinar el valor de \(k\) deberíamos de tener otra condicion inicial, por lo que propondremos lo siguiente:

Condición inicial propuesta

Se tomó la siguiente medición de las ratas infectadas: \(R(t=5) = 10\)

Si esto lo reemplazamos en (4) (reemplazando previamente el valor de \(C\)):

\[\frac {10}{500-10} = \frac {1}{99} e^{2500k}\]
\[\frac {99}{49} = e^{2500k}\]
\[\ln \frac {99}{49} = 2500k\]
\[k = \frac {\ln 99 - \ln 49}{2500} \approx 2.81 \times 10^{-4}\]

Solución particular

Reemplazando \(k\) en (6) nos queda la solución particular al modelo matemático planteado inicialmente:

(7)\[R_{(t)} = \frac {500}{ \frac {99}{e^{0.1405 t}} + 1 }\]

Ahora solo nos queda averiguar la principal incógnita del problema, en la que debemos averiguar para qué valor de \(t\) se cumple que \(R(t)=250\). Reemplazamos esto último en (7):

\[250 = \frac {500}{ \frac {99}{e^{0.1405 t}} + 1 }\]
\[\frac {99}{e^{0.1405 t}} + 1 = \frac {500}{250}\]
\[\frac {1}{99} e^{0.1405 t} = 1\]
\[ \begin{align}\begin{aligned}e^{0.1405 t} = 99\\0.1405 t = \ln 99\end{aligned}\end{align} \]
(8)\[t = \frac {\ln 99}{0.1405} \approx 32.705\]

Resultado final

Por lo tanto, el tiempo que le tomará a la mitad de la población adquirir la enfermedad es \(t=32.705\) unidades de tiempo.

Interpretación gráfica

Vemos que la primer condicion inicial (CI)(en el gráfico se representa con un punto llamado \(A(0, a_y)\)) hace variar el valor de \(C\). También, vemos que si mantenemos fijo el valor de la segunda CI (representada con un punto llamado \(B(5 , b_y)\)), variando \(a_y\) se modifica también el valor de \(k\). Al variar \(b_y\) se consigue cambiar el valor de \(k\).



Vemos que el valor de \(t\) en \(R(t)=250\) es ligeramente distinto al calculado en el desarrollo, esto se debe a que hubo un error de redondeo cuando se calculó \(k\) en el desarrollo, si se hubieran mantenido las expresiones sin calcular y se resolvía utilizando la mayor cantidad de decimales posible, el resultado sería identico al mostrado en la gráfica.

En el siguiente gráfico, no mantendremos fijo la posición de \(B\). Modificaremos el valor de \(k\) con un deslizador. Esto los haremos para mostrar cómo al variar \(a_y\) la curva solución se desplaza y «sigue» las trazas dada por los vectores del campo descripto por la solución general.



Ejercicio 2

Dennis G. Zill y Warren S. Wright (2015). Ecuaciones Diferenciales con problemas con valores en la frontera. (8va ed.). Cengage Learning.

Enunciado

Se posee un tanque con 300 litros de salmuera y 50 kg de sal disuelta en un inicio. Al mismo se le quiere variar la concentración de sal mediante el ingreso de salmuera de una concentración distinta y la expulsión del líquido del tanque al mismo ritmo del que entra.

Con esto se quiere demostrar que la tasa de variación instantánea de la cantidad de sal en el tanque responde directamente a la diferencia de la razón de entrada de sal con la de salida.

En este caso, la salmuera ingresante tiene una concentración de 2kg/litro de sal. El ritmo con que ingresa es de 3 litros/minuto.

Además de demostrar lo mencionado previamente, se quiere averiguar si hay una tendencia en la cantidad de sal dentro del tanque en un período largo de tiempo, y si la hay, saber su valor.

Por ultimo, ¿Cuánta sal se depositará en en el tanque si el flujo de entrada de la salmuera fuera mayor que el flujo de salida de la mezcla?

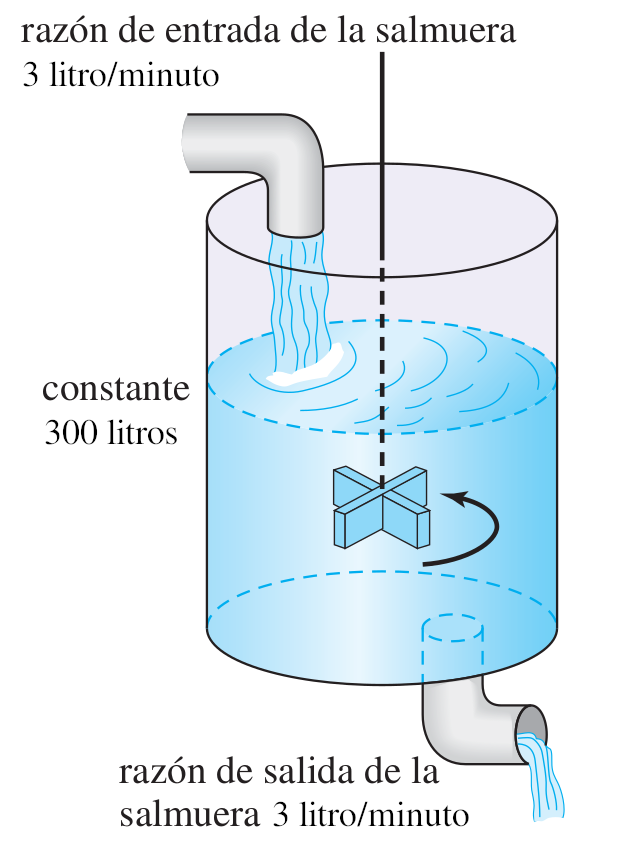
tanque

Imagen ilustrativa. Zill y Wright. Ecuaciones Diferenciales con problemas con valores en la frontera (valores editados).

Desarrollo

Desarrollo (Parte A)

Sea \(A(t)\) la cantidad de sal, medida en kilogramos, dentro del tanque en el tiempo \(t\). Además, el enunciado nos dice que \(A(t=0) = 50\). También sabemos que \([A(t)] = kg\).

Luego, el enunciado nos dice lo siguiente:

se quiere demostrar que la tasa de variación instantánea de la cantidad de sal en el tanque responde directamente a la diferencia de la razón de entrada de sal con la de salida

Lo cual, se puede modelizar matemáticamente con la siguiente ecuación diferencial:

(9)\[\frac {dA}{dt} = R_{entra} - R_{sale}\]

Donde:

  • \(R_{entra}\) es la razón de entrada de la sal con la que entra en el tanque

  • \(R_{sale}\) es la razón de salida de la sal con la que sale del tanque

A su vez, \(R_{entra}\), que se mide en \(\frac {kg}{minuto}\), es el producto de la concentración de la afluencia de sal y la tasa de flujo de fluido. Ambas magnitudes, según el enunciado, valen \(2 \frac {kg}{litro}\) y \(3 \frac {litro}{minuto}\) respectivamente, entonces:

(10)\[R_{entra} = 2 \frac {kg}{litro} · 3 \frac {litro}{minuto} = 6 \frac {kg}{minuto}\]

Como la solución que sale del tanque lo hace con la misma intensidad que con la que entra, la cantidad de litros de salmuera en el tanque al tiempo \(t\) es una constante de 300 litros.

Sea \(c_{(t)}\) la concentración de la sal en el tanque así como en la mezcla de salida, y queda definida de la siguiente manera:

(11)\[c_{(t)} = \frac { A_{(t)} }{300} \frac {kg}{litro}\]

Recordemos que \(A(t)\) es la cantidad de sal dentro del tanque en un tiempo \(t\).

Luego, la razón de salida de sal \(R_{sale}\), muy similar a la razón de entrada, es el producto de la concentración de sal en el tanque y el flujo de salida de la solución. Estas magnitudes valen \(c_{(t)}\) y \(3 \frac {litro}{minuto}\), es decir:

\[R_{sale} = c_{(t)} · 3 \frac {litro}{minuto}\]

Reemplazamos la definición de \(c_{(t)}\), simplificamos y nos queda:

(12)\[R_{sale} = \frac { A_{(t)} }{100} \frac {kg}{minuto}\]

Con ambas razones definidas, sustituimos (10) y (12) en (9):

\[\frac {dA}{dt} = \left( 6 \frac {kg}{minuto} \right) - \left( \frac { A_{(t)} }{100} \frac {kg}{minuto} \right)\]

Reacomodando:

\[\frac {dA}{dt} + \frac { A_{(t)} }{100} \frac {kg}{minuto} = 6 \frac {kg}{minuto}\]

Vemos que todos los términos, en ambos miembros, poseen las mismas unidades (ya que \(\left[ \frac {dA}{dt} \right] = \frac {kg}{minuto}\) ), y por lo tanto, para simplificar el cálculo, dejaremos de mencionarlas de ahora en más, a no ser que sea necesario explicitarlas. Entonces:

Modelo matemático

La siguiente ecuación es la modelización matemática del problema planteado, la cual es una ecuación diferencial lineal de primer orden.

(13)\[\frac {dA}{dt} + \frac { A_{(t)} }{100} = 6\]

Para encontrar la función solución \(A(t)\) se utiliza método del factor integrante. Según (13) se definen:

\[p_{(t)} = \frac {1}{100}\]
\[q_{(t)} = 6\]

Sea \(u_{(t)}\) el factor integrante definido como:

\[u_{(t)} = e ^ {\int p_{(t)} dt} = e ^ {\frac {1}{100} \int dt}\]
(14)\[u_{(t)} = e^{\frac {t}{100}}\]

Multiplicando ambos miembros de (13) por el factor integrante nos queda:

\[\frac {dA}{dt} · u_{(t)} + \frac { A_{(t)} }{100} · u_{(t)} = 6 · u_{(t)}\]

Sustituimos con (14):

\[\frac {dA}{dt} · e^{\frac {t}{100}} + \frac { A_{(t)} }{100} · e^{\frac {t}{100}} = 6 · e^{\frac {t}{100}}\]

Notamos que el miembro izquierdo de la expresión anterior es igual a la derivada del producto entre \(A(t)\) y \(e^{\frac {t}{100}}\), por lo que la expresión anterior se puede reescribir como:

\[\frac {d}{dt} (A_{(t)} · e^{\frac {t}{100}}) = 6 · e^{\frac {t}{100}}\]

Integramos ambos miembros:

\[\int \frac {d}{dt} (A_{(t)} · e^{\frac {t}{100}}) dt = \int 6 · e^{\frac {t}{100}} dt\]
\[A_{(t)} · e^{\frac {t}{100}} = 600 · e^{\frac {t}{100}} + C\]

Tal que \(C\) es una constante de integración.

Solución general

Por último, despejando \(A(t)\), obtenemos la solución general de la ecuación diferencial lineal de primer orden:

(15)\[A_{(t)} = 600 + C · e^{\frac {-t}{100}}\]

Por la condición inicial dada en el enunciado, sabemos que \(A(t=0) = 50\). Sustituimos esta condición inicial en (15):

\[50 = 600 + C · e^{\frac {0}{100}}\]
\[-550 = C · 1 \implies C = -550\]

Solución particular

Reemplazamos \(C\) en (15) y obtenemos la solución particular de nuestro modelo planteado inicialmente:

(16)\[A_{(t)} = 600 - 550 · e^{\frac {-t}{100}}\]

Ahora, resolveremos la primer incógnita de nuestro problema, y es, si hay o no una tendencia en la cantidad de sal depositada pasado un período largo de tiempo. Para esto observamos la cantidad de sal depositada en el tanque para distintos valores temporales.

\(t\) [minutos]

\(A(t)\) [kg]

\(t\) [minutos]

\(A(t)\) [kg]

0

50

200

525.56

50

266.4

300

572.61

100

397.66

400

589.92

150

477.27

500

596.29

Se puede observar que conforme t aumenta la cantidad de sal depositada alcanza un límite de \(A=600kg\), por lo tanto, calculamos el límite de \(A(t)\) para cuando \(t \implies \infty\):

\[lim_{t \to \infty} A_{(t)} = lim_{t \to \infty} \left( 600 - 550 · e^{\frac {-t}{100}} \right) = 600 - \frac {500}{\infty} = 600\]

Respuesta final

La cantidad de sal en un período largo de tiempo tiende a 600kg

Vemos que el gráfico de \(A(t)\) nos muestra la misma tendencia:

Desarrollo (Parte B)

Por último, se pide lo siguiente:

¿Cuánta sal se depositará en en el tanque si el flujo de entrada de la salmuera fuera mayor que el flujo de salida de la mezcla?

En el análisis que conduce a la ecuación (13) se tomo que \(r_{entra} = r_{sale}\) (es decir, que la tasa de entrada y salida de líquido era la misma), pero esta relación puede ser de 3 formas:

  1. \(r_{entra} = r_{sale}\)

  2. \(r_{entra} > r_{sale}\)

  3. \(r_{entra} < r_{sale}\)

Para este caso, la forma a tomar es de \(r_{entra} > r_{sale}\).

Entonces supongamos que la solución mezclada se bombea hacia afuera con una tasa de flujo de mezcla más lenta de \(2 litro/minuto\), por lo que se acumulará en el tanque con la razón \(r_{entra} - r_{sale} = (3-2) litro/minuto = 1 litro/minuto\).

Si evaluamos el líquido dentro del tanque después de \(t\) minutos será: \(1 \frac {litro}{minuto} · t · minuto = t · litro\)

Vemos que la cantidad de fluido incrementa con el tiempo, por lo que modificará (11) y se vuelve a definir \(c_{(t)}\) como:

(17)\[c_{(t)} = \frac { A_{(t)} }{300 + t} \frac {kg}{litro}\]

Esto también obliga a reescribir (12):

\[R_{sale} = c_{(t)} · r_{sale} = c_{(t)} · 2 \frac {litro}{minuto}\]

Reemplazamos la definición de \(c_{(t)}\):

(18)\[R_{sale} = \frac { 2 A_{(t)} }{300 + t} \frac {kg}{minuto}\]

Modelo matemático (nuevo)

La ecuación diferencial (13) ahora es

(19)\[\frac {dA}{dt} + \frac { 2 A_{(t)} }{300 + t} = 6\]

Aplicando el mismo método de resolución, vemos que su factor integrante es:

\[u_{(t)} = e ^ {\int \frac {2}{300 + t} dt}\]
(20)\[u_{(t)} = (300 + t)^2\]

Luego multiplicamos ambos miembros de (19) por el factor integrante:

\[\frac {dA}{dt} · u_{(t)} + \frac { 2 A_{(t)} }{300 + t} u_{(t)} = 6 u_{(t)}\]
\[\frac {dA}{dt} · (300 + t)^2 + \frac { 2 A_{(t)} }{300 + t} (300 + t)^2 = 6 (300 + t)^2\]
\[\frac {dA}{dt} · (300 + t)^2 + 2 A_{(t)} · (300 + t) = 6 (300 + t)^2\]

Vemos que el primer miembro se puede reescribir de la siguiente manera:

\[\frac {d}{dt} (A_{(t)} · (300 + t)^2) = 6 (300 + t)^2\]

Integramos ambos miembros:

\[ \begin{align}\begin{aligned}A_{(t)} · (300 + t)^2 = 6 \int (300 + t)^2 dt\\A_{(t)} · (300 + t)^2 = 2 (300 + t)^3 + C\end{aligned}\end{align} \]

Solución general (nueva)

Despejando \(A(t)\), obtenemos la solución general

(21)\[A_{(t)} = 600 + 2t + C · (300 + t)^{-2}\]

Resolviendo para \(A(t=0) = 50\):

\[50 = 600 + 0 + C · (300 + 0)^{-2}\]
\[-550 · 300^2 = C\]
\[C = - 4.95 · 10^7\]

Solución particular (nueva)

Reemplazamos \(C\) en (21) y obtenemos la solución particular

(22)\[A_{(t)} = 600 + 2t - 4.95 · 10^7 · (300 + t)^{-2}\]

Graficamos esta solución particular y su correspondiente campo vectorial de la solución general.

Como era de esperar, se muestra que con el tiempo se acumula la sal en el tanque. Si calculamos su límite:

\[lim_{t \to \infty} A_{(t)} = lim_{t \to \infty} \left( 600 + 2t - 4.95 · 10^7 · (300 + t)^{-2} \right) = 600 + \infty + 0 = \infty\]

Respuesta final

La cantidad de sal en un período prolongado de tiempo tiende a infinito cuando el flujo de entrada de la salmuera es mayor que el flujo de salida de la mezcla.

Información adicional